[ベスト] 超複素数 286102-数学 超複素数
佐藤超関数の紹介 桂田祐史 17年7月6日, 19 年7 月22 日 「複素関数」は数学的にかなり厳密な議論をしたのに比べると、「応用複素関数」は少々ゆ るい議論に止めているけれど(同じレベルで厳密な議論をするための準備が無理なため)、この 特殊な幾何的対象と「数」概念の拡張から立ち現れる、整数論と超弦理論との関連 1 発表概要 従来より、数論幾何の分野では、有理数のみを係数にもつ方程式で与えられた一群の幾何的対象につき、対応するモジュラー形式が存在することが知られてき cuda上で複素数入力のハンケル関数 (complex Bessel function, Hankel function)を扱いたかったんでメモ。 四角い車輪の再発明なので用途に困ったとき以外は素直にboostライブラリの関数や、fortranライブラリの流用を検討すること。 complex_bessel GitHub scipyspecialhankel2 SciPy Cyclic Hankel Functions boostorg amos http//wwwnetliborg/amos/
オイラーの公式 三角関数 複素指数関数 虚数が等式として集約されるまでの物語 空間情報クラブ 株式会社インフォマティクス
数学 超複素数
数学 超複素数-超複素数入門 多元環へのアプローチ ИЛКантор, АССолодовников著 ;;;z) = ∑1 k=0 ( )k( )k)k(1)k zk (51) をガウスの超幾何級数という ここで, s 2 C およびk = 0;1;2;
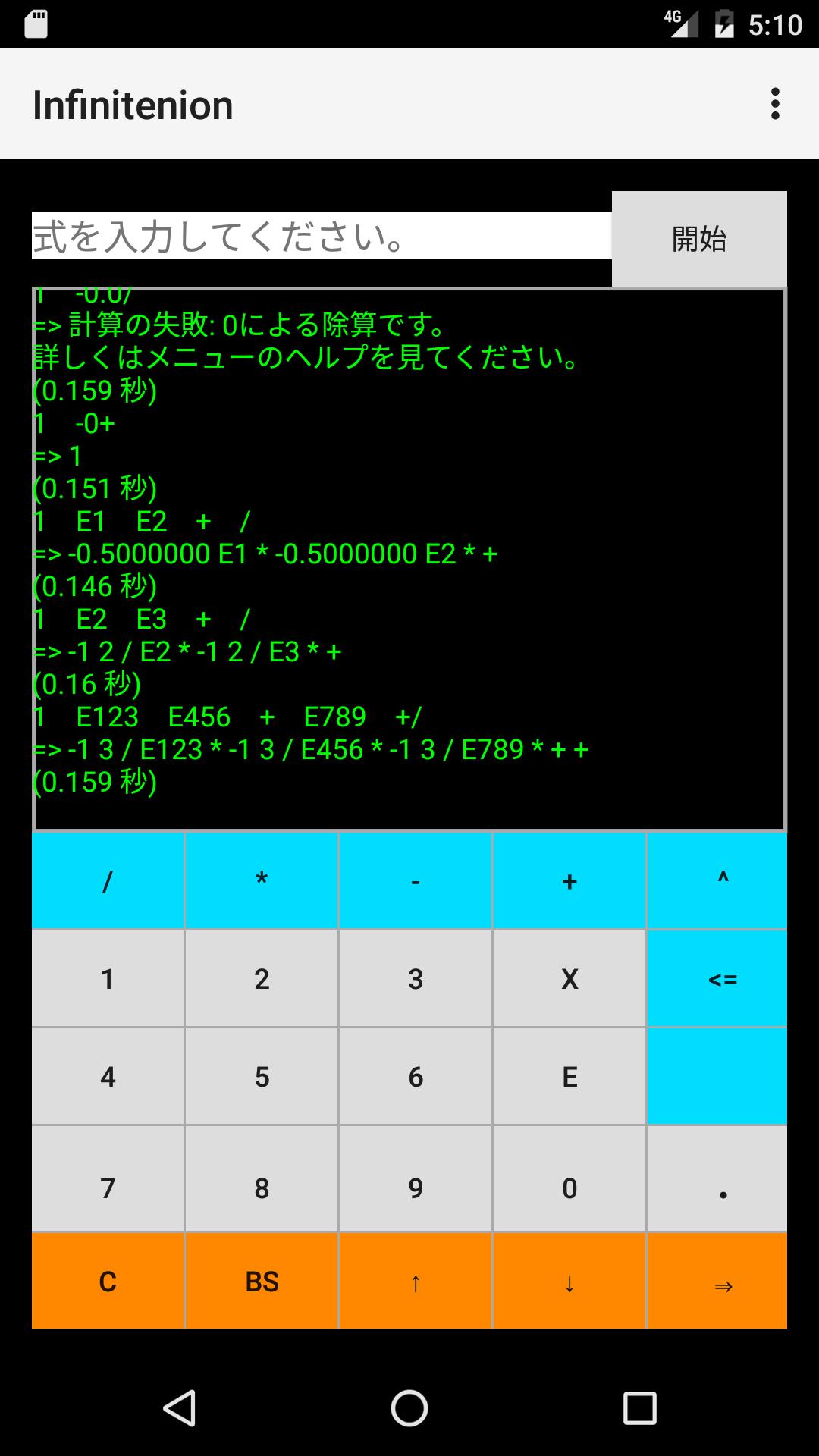



無限次元超複素数電卓 Infinitenion Dlya Android Skachat Apk
もちろん,三元数は存在しないので,六元数も存在しないが,ケイリー・ディクソンの2重化法 C=R+iR H=C+iC (複素数の複素化) を適用して構成される超複素数体系が,八元数 O=H+iH (四元数の複素化) 数靈76)という名の、超複素数。 1843年にアイルランドの数学者ハミルトンが発見した数、ということです。 ハミルトン数(162) という別名も、あるにはあるようです。 虚数単位を、 i 、 j 、 k の3つの文字で別々に考えて、2 C をパラメータとするz のべき級数 F( ;
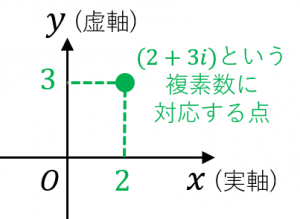
超複素数は 複素数(i^2=1を満たすabi)、 二重数(i^2=1を満たすabi)、 双対数(i^2=0を満たすabi)、 4元数、 8元数 ケーレー環 があるのですね。これらはみな多元環の構造をなすのですね。 これら以外には以外には超複素数と呼ばれるものは存在しないのでしょうか?複素数(Complex Numbers) 例えば,z = 3 2i とすると,z, z, z は右図のようになる。 複素数 z = a bi と共役な複素数 a bi を z で表す。 複素数とは? 複素数が等しいとは?(複素数の相等) 複素数の四則演算 複素数の平面 共役(きょうやく)な複素数とは?Contribute to tannakaken/CayleyDickson development by creating an account on GitHub
超複素数の世界 超複素数の世界 数の世界は、自然数から負の数へ、有理数から無理数へ、実数から複素数へと拡大してきました。 如何にしてその数が発見されたのか、あるいは、数の概念を拡張するのにどれだけ長くかかったかなどは大変興味深いテーマです。 複素数は難解とか複雑な数ということではなく、実数と虚数という二つの項をもつ数(x+yi)のこと数の拡張について知りたく思っております。 自然数に負数の概念を加えると整数 ↓ 整数に分数の概念を加えると有理数 ↓ 有理数に無理数の概念を加えると 質問No目次 第1部 超複素数(複素数;数a+biにおける別の算法;4元数;4元数とベクトル代数;超複素数;二重化、ケーリー数;多元環) 第2部 n次元ベクトル(n次元ベクトル空間An;空間Anの基底;部分空間;連立同次1次方程式に関する補題;スカラー積;正規直交基底、直交変換) 第3部 4つの特別



1



複素数 Wikipedia
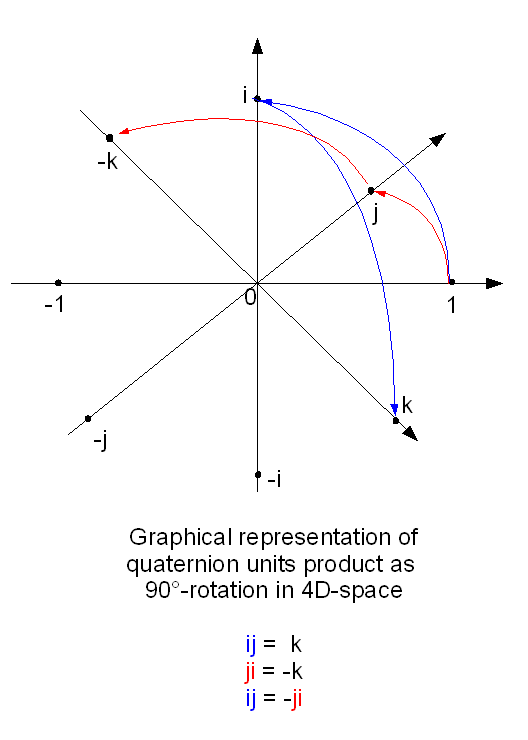
数学特論II (担当 天野勝利) 18年12月6日~19年1月24日 5 ガウスの超幾何関数 51 ガウスの超幾何級数 複素数 ;超複素数入門―多元環へのアプローチ Kantor,I.L. / Solodovnikov,A.S.著 / 浅野 洋監訳 / 笠原 久弘訳 森北出版 (1999/09発売) ただいまウェブストアではご注文を受け付けておりません。 サイズ A5判/ページ数 172p/高さ 22cm 商品コード すると自然な疑問として, 「複素数体」と呼ばれる複素数全体の集合に「第2の虚数単位j」 (及びその実数倍)を付け足した数の世界「超複素数体」を与え, 12 22 32 が同様に因数分解できるかという問が考えられる 実は付け足す虚数単位が一つでは「数学的な不都合」 (説明は後ほど)が生じ, そこで「第2, 第3の虚数単位j, k」 (図1参照)を与えると という分解ができる




超複素数入門 多元環へのアプローチ Kantor I L Solodovnikov A S 洋 浅野 久弘 笠原 本 通販 Amazon




高校数学 共役複素数の図形的意味と性質 複素数の実数条件 純虚数条件 受験の月
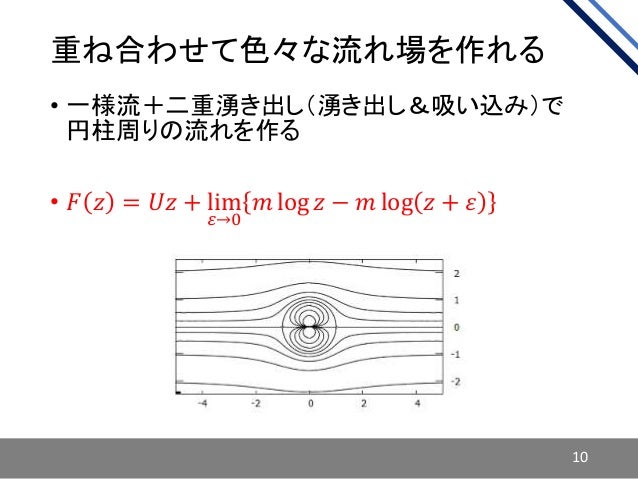
ーマル成分は殆ど励起されていないので超流体の中に生じた個々の渦糸の運動を問題にしう ると考えられる さて,こ の超流体の状態を表すオーダーパラメーターは巨視的な複素数の波動関数ψ(r, のであ超関数の演算 4 等式: 超関数 は,実数(または複素数) に対して 何らかの値を定義するものではない。しかし, 超関数 と関数(または超関数) に対して とは,区間 以外ではゼロとなる全てのテスト関数 に対して下記が成り立つことと定義する一般に, 元数を 超複素数 と言いますが,ここでは超複素数の一般論には深入りしません.結論だけ述べると,五元数や六元数では乗法が上手く定義できず,四元数の次に体をなす超複素数は 八元数 です.八元数はハミルトンの友人のグレーヴスによって




複素数 Wikipedia




超複素数の意味 用法を知る Astamuse
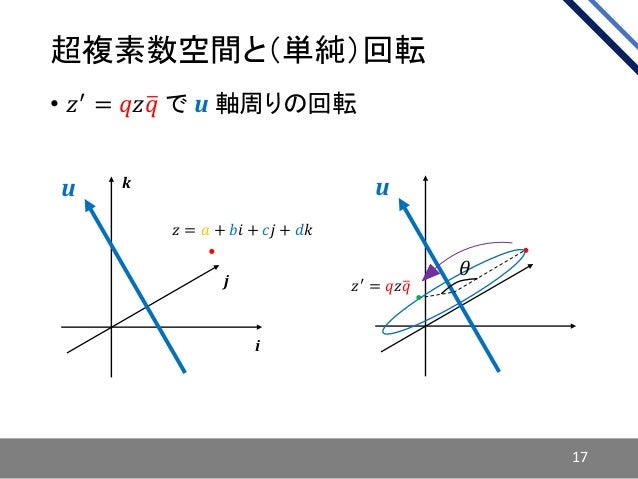
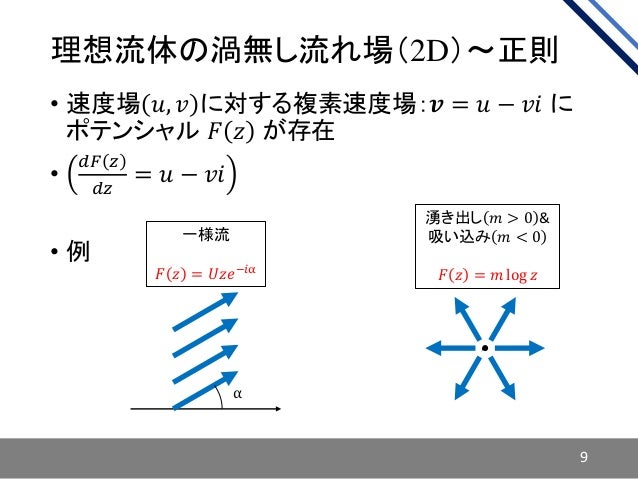
(証明は「複素関数」の講義ノートに書いてある。) 221 ∫1 0 f(x) dx ここでは、半無限区間0;1) 上の積分 ∫1 0 f(x) dx の値を計算する方法を紹介する。 (「複素関数」ではf が偶関数の場合に、 ∫1 0 f(x) dx = 1 2 ∫1 1 f(x) dx として、(1 ;1) みなさんこんにちは!武田塾京都北大路校講師の秦コチラです! 高校数学で習う訳のわからないものの代表、「虚数・複素数」 そんな虚数・複素数が役立っている身近な例を紹介します。 *数3の分野を含むので習っていない人は何となく読み進めてもらえばと思います。 12 超複素数 • 𝑧 = 𝑎 𝑏𝑖 𝑐𝑗 𝑑𝑘 • 𝑖 (𝑎, 𝑏, 𝑐, 𝑑 ∈ 𝑹, 𝑖2 = 𝑗2 = 𝑘2 = 𝑖𝑗𝑘 = −1, • 𝑖 (𝑖𝑗 = 𝑘, 𝑗𝑘 = 𝑖, 𝑘𝑖 = 𝑗, 𝑗𝑖 = −𝑘, 𝑘𝑗 = −𝑖, 𝑖𝑘 = −𝑗) 12 13 超複素数 • 𝑧 = 𝑎 𝑏𝑖 𝑐𝑗 𝑑𝑘 • 𝑖 (𝑎, 𝑏, 𝑐, 𝑑 ∈ 𝑹, 𝑖2 = 𝑗2 = 𝑘2 = 𝑖𝑗𝑘 = −1, • 𝑖 (𝑖𝑗 = 𝑘, 𝑗𝑘 = 𝑖, 𝑘𝑖 = 𝑗



ゲームの中に 虚数あり




超複素数
大学単位 複素数平面が超わかる! 4点が同一円周上にある条件の復習(高校数学Ⅲ) 投稿日:年2月9日 複素数平面が面白いぐらいわかるようになる! 動画リスト 「複素数平面」が苦手すぎる! 「複素数平面」を一から丁寧に勉強し数学における超複素解析(ちょうふくそかいせき、英 hypercomplex analysis )は、実解析や複素解析を 函数の引数 (英語版) が多元数(超複素数)である場合の研究に拡張するものである。超複素数系に関するカテゴリ。 カテゴリ「超複素数系」にあるページ このカテゴリには 16 ページが含まれており、そのうち以下の 16 ページを表示しています。



1




淡中 圏 Ar Twitter C93 コミケ 数学 宣伝です コミケ三日目ニ 48aで 数学同人誌 The Dark Side Of Forcing Vol 10を売ります 今回の内容は 公理的集合論 型理論 圏論 Haskell 超複素数 マイリトルポニー そしてモンティパイソン となっております
この答えは驚くべきことに「1/12」になると、18世紀の数学者、オイラーが複素数の解析学を用いて導き出した。 今回の数字「11次元」を導き出す重要な小道具である。 この「次元」とは何か。 「1点の位置を決めるのに必要な数値の個数」という説明がわかりやすいだろう。 1次元は直線の世界で、原点からの距離だけで位置は決まる。 2次元は平面で縦と横の2個複素数を超えて 四元数と八元数 植田一石 1 自然数から整数へ あらゆる数の体系の中で最初に現れるのは自然数(natural number) であり、ものを「数える」のに使われる。 あまりにも基本的なので意識することは少ないが、数は高度に抽象的な概念である。を複素数にとって、次のように超関数を返すようにすることで定義を拡張する。実際、通常のフーリエ変換が 可能な場合は、これは整合的な結果を返す。 (∫ f(x)exp(ipx)dx) (p) = 1Imp>0 (∫ 0ϵ 1 ϵ f(z)exp(ipz)dz ∫ 0 ϵ 1 ϵ f(z)exp(ipz)dz) (5) 1Imp




無限次元超複素数電卓 Infinitenion Dlya Android Skachat Apk




複素数平面の基礎はこの動画でつかむ テスト前の救世主 Okenavi
笠原久弘訳 森北出版, 117 POD版複素数と方程式が超わかる! 複素数の範囲での因数分解 (高校数学Ⅱ・B) Duration 448 超わかる!高校数学 II・B 30,210 views 複素数の範囲とは何ですか?? あと、いきなりiご出てきたのはで表される一般化関数である.そして,複素解析 関数F z を超函数f x の定義関数とよぶ.数 値積分の応用には超函数の積分の定義が必要であ るが,区間I上の超函数f x の積分は次のよう に,定義関数F z の複素積分によって定義され る. f x dx=




無限次元超複素数電卓 Infinitenion Dlya Android Skachat Apk




超複素数の意味 用法を知る Astamuse
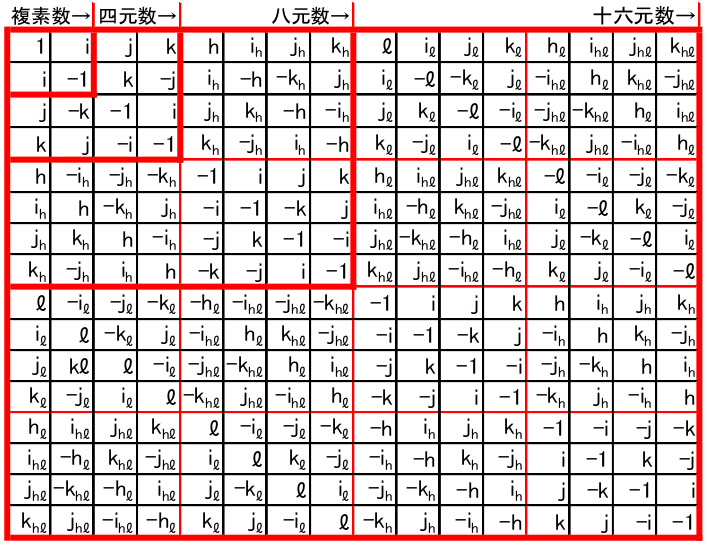
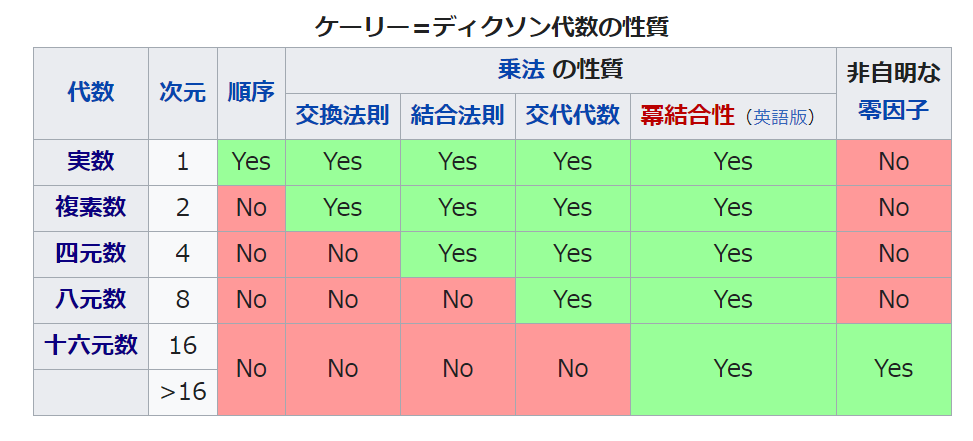
Amazoncom で、超複素数入門 POD版 の役立つカスタマーレビューとレビュー評価をご覧ください。ユーザーの皆様からの正直で公平な製品レビューをお読みください。超複素数 本研究で扱う超複素数は、4次元以下で結合則を満たす代数系に限られる。 Clifford algebra と CayleyDickson の系列は有名な超複素数の構成法である。 表の代数系は全て環であり、結合則、分配則を満たす。 0以外の元が常に逆数を持つ場合は特に体と呼ばれる。 紹介する超複素数 hyperbolic number hyperbolic quaternion split quaternion本発明のある側面は、ギャップエネルギーを複素数化し、MattisBardeen方程式を使って超伝導膜の表面抵抗を推測することを特徴とする超伝導膜表面抵抗推測方法にある。 例文帳に追加 In the method for guessing a surface resistance of a superconductive
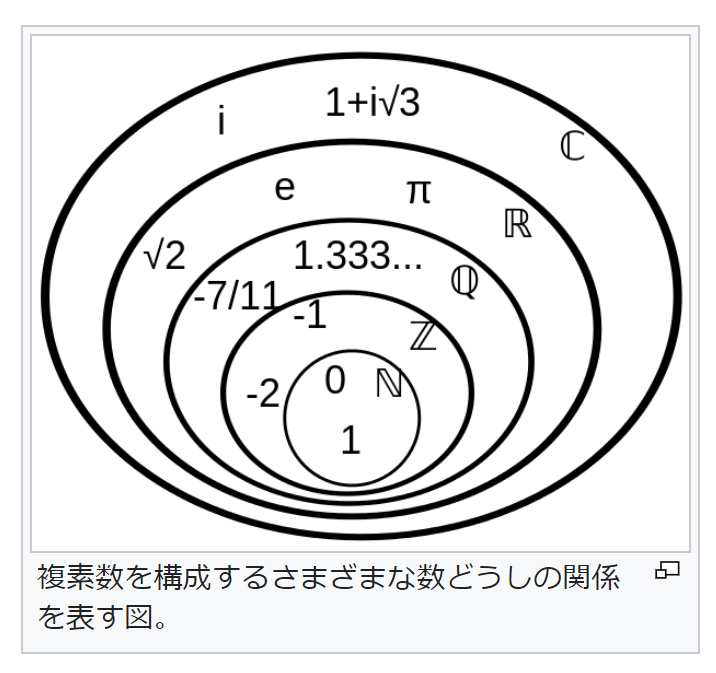



数体系の特徴 Qiita




京都市の予備校 武田塾 数学が実生活で役立っている身近な例 予備校なら武田塾 京都北大路校




超複素数




複素数 Wikipedia




複素数 Wikipedia




超複素数




複素数平面って何 数学iii 複素数平面3 高校数学理論講座 Youtube




超複素数入門 Pod版 森北出版株式会社




数の世界 自然数から実数 複素数 そして四元数へ 松岡 学 ブルーバックス 講談社book倶楽部
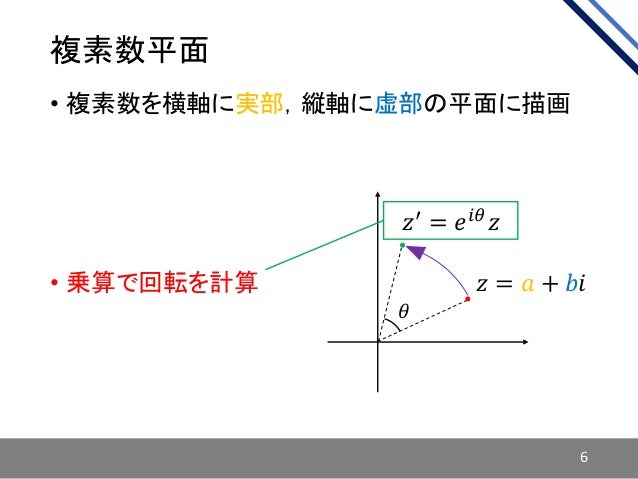



超複素数




超目玉 Mathematics Without Rote Learning 覚えない数学 複素数平面 曲線 テキスト1冊 解説dvd 3枚 Drpietrorotondi Org




Category 超複素数系 Page 1 Japaneseclass Jp




超複素数のお話 Mathlog



四元数 Wikipedia




数学 数学iii 複素数平面演習 複素数を完璧に Youtube




高校生からわかる複素解析 涌井良幸 とね日記




複素数 Wikipedia




超複素数



ゲームの中に 虚数あり




複素数 Wikipedia




虚数で回転を表現しよう 高校数学を100倍楽しく Youtube




淡中 圏 Ar Twitter C93 コミケ 数学 宣伝です コミケ三日目ニ 48aで 数学同人誌 The Dark Side Of Forcing Vol 10を売ります 今回の内容は 公理的集合論 型理論 圏論 Haskell 超複素数 マイリトルポニー そしてモンティパイソン となっております




無限次元超複素数電卓 Infinitenion Apk Download For Android Latest Version 1 1 4 Jp Tannakaken Infinitenion




超複素数入門 多元環へのアプローチ Kantor I L Solodovnikov A S 洋 浅野 久弘 笠原 本 通販 Amazon




Category 超複素数系 Page 1 Japaneseclass Jp



多重複素数入門 七誌の開発日記




超複素数 四元数と八元数 自己の輝き発見 カタカムナ




ヤフオク 複素数の中古品 新品 未使用品一覧




超複素数




複素数 複素数の概要 Weblio辞書




Category 超複素数系 Page 1 Japaneseclass Jp




超複素数




Category 超複素数系 Page 1 Japaneseclass Jp




複素数平面は1時間で解けるようになる 外資系コンサルタントが主夫になったら




超複素数入門 多元環へのアプローチ pod版の通販 I L Kantor A S Solodovnikov 紙の本 Honto本の通販ストア



四元数体と正の整数を4つの整数の平方和で書く問題をめぐって 基幹理工学部 数学科 成田 宏秋 早稲田大学 基幹理工学部 研究科




複素数平面 数がく部



1




Category 超複素数系 Page 1 Japaneseclass Jp




数学関連本13冊まとめ 微分積分 リーマン幾何学 相対性理論 超複素数入門 電磁気学等 数学 売買されたオークション情報 Yahooの商品情報をアーカイブ公開 オークファン Aucfan Com



3dmandelbrot M28a




超複素数入門 Pod版 森北出版株式会社




複素数平面の基礎はこの動画でつかむ テスト前の救世主 Okenavi



Category 超複素数系 Page 1 Japaneseclass Jp




複素数 Wikipedia



複素数 Wikiwand




淡中 圏 Ar Twitter C93 コミケ 数学 宣伝です コミケ三日目ニ 48aで 数学同人誌 The Dark Side Of Forcing Vol 10を売ります 今回の内容は 公理的集合論 型理論 圏論 Haskell 超複素数 マイリトルポニー そしてモンティパイソン となっております



ゲームの中に 虚数あり




淡中 圏 Ar Twitter C93 コミケ 数学 宣伝です コミケ三日目ニ 48aで 数学同人誌 The Dark Side Of Forcing Vol 10を売ります 今回の内容は 公理的集合論 型理論 圏論 Haskell 超複素数 マイリトルポニー そしてモンティパイソン となっております




ヤフオク 複素数の中古品 新品 未使用品一覧
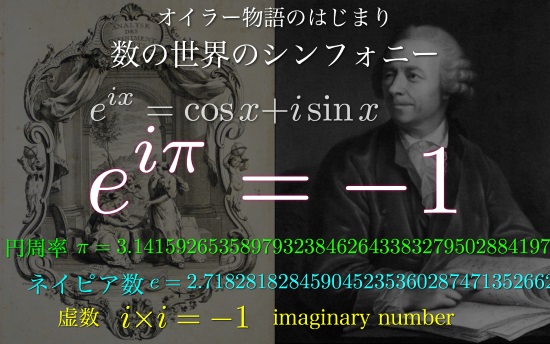



オイラーの公式 三角関数 複素指数関数 虚数が等式として集約されるまでの物語 空間情報クラブ 株式会社インフォマティクス




淡中 圏 Ar Twitter C93 コミケ 数学 宣伝です コミケ三日目ニ 48aで 数学同人誌 The Dark Side Of Forcing Vol 10を売ります 今回の内容は 公理的集合論 型理論 圏論 Haskell 超複素数 マイリトルポニー そしてモンティパイソン となっております
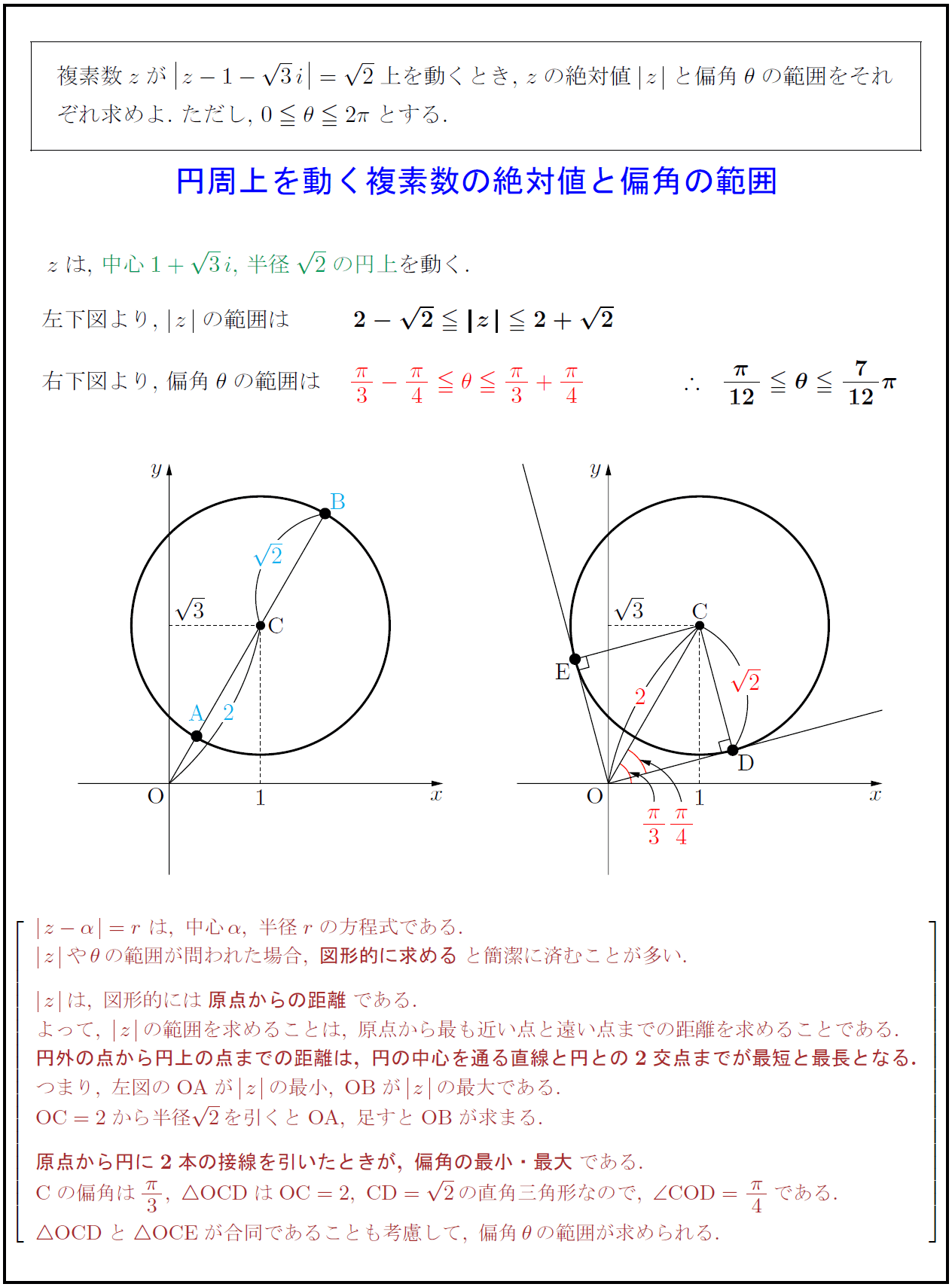



高校数学 円周上を動く複素数の絶対値と偏角の範囲 受験の月




超複素数入門 Pod版 洋 浅野 久弘 笠原 本 通販 Amazon




オイラーの公式 三角関数 複素指数関数 虚数が等式として集約されるまでの物語 空間情報クラブ 株式会社インフォマティクス




複素数平面まとめ 高校数学 複素数平面 41 Youtube




超複素数入門 多元環へのアプローチ Kantor I L Solodovnikov A S 洋 浅野 久弘 笠原 本 通販 Amazon




複素数平面の公式まとめ 極形式 回転 ドモアブルの定理 理系ラボ




C で少し便利かもしれない行列ライブラリと超複素数ライブラリ作ってみた Qiita




超複素数




超複素数入門 Pod版 森北出版株式会社




超複素数




複素数平面 数がく部




超複素数入門 Pod版 森北出版株式会社



超複素数




ヤフオク 複素数 数学 の中古品 新品 古本一覧




超複素数




七誌 比較的平易に複素数 四元数 クリフォード代数を導入している 複素数の逆数は行列表現で逆行列として導出すれば簡単なのに気付いた Clifford Algebra And Spinor Valued Functions T Co Wndwo9o6fy T Co Huc4piolnw



数体系の特徴 Qiita




超複素数



超複素数




z会 数学 複素数平面1 ポイント整理の学習



京都市の予備校 武田塾 数学が実生活で役立っている身近な例 予備校なら武田塾 京都北大路校




複素数平面まとめ 高校数学 複素数平面 41 Youtube




Unity初心者でも 数学苦手でも 角度のquaternion表現を理解したい Qiita




複素数平面は1時間で解けるようになる 外資系コンサルタントが主夫になったら




Category 超複素数系 Page 1 Japaneseclass Jp




複素数平面の公式まとめ 極形式 回転 ドモアブルの定理 理系ラボ




超複素数



Search Q E8 87 E7 B4 A0 E6 95 B0 E5 9b 9e E8 Tbm Isch




超複素数入門 多元環へのアプローチ Kantor I L Solodovnikov A S 洋 浅野 久弘 笠原 本 通販 Amazon



無限次元超複素数電卓 Infinitenion Androidアプリ Applion




超複素数入門 Pod版 森北出版株式会社




超複素数の意味 用法を知る Astamuse




虚数で回転を表現しよう 高校数学を100倍楽しく Youtube




複素数 Wikipedia




楽天ブックス 入門複素関数 川平 友規 本



超複素数




超複素数




超複素数 四元数と八元数 自己の輝き発見 カタカムナ


コメント
コメントを投稿